 Chủ đề 9. Trục đối xứng. Tâm đối xứng
Chủ đề 9. Trục đối xứng. Tâm đối xứng
Lý thuyết
Những hình có một điểm O sao cho khi quay nửa vòng quanh điểm O ta được vị trí mới của hình chồng khít với vị trí ban đầu (trước khi quay) thì được gọi là hình có tâm đối xứng và điểm O được gọi là tâm đối xứng của hình.
Tâm đối xứng của một số hình phẳng
Tâm đối xứng của hình bình hành, hình thoi, hình vuông, hình chữ nhật là giao điểm của hai đường chéo.
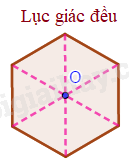
Tâm đối xứng của hình lục giác đều là giao điểm của các đường chéo chính.
Bài tập
Bài 1:
Chữ cái nào trong mỗi từ sau có tính đối xứng? Với mỗi từ, hãy nêu tên tỉnh thành tương ứng:
a) H O A B I N H b) N G H E A N
c) B E N T R E d) B A C K A N
e) Q U A N G T R I g) D A N A N G
Bài 2:
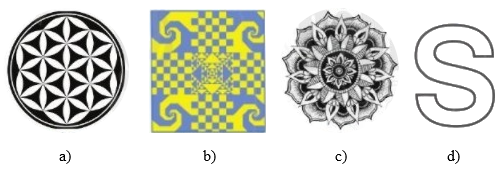
Trong các hình dưới đây, hình nào có tâm đối xứng?
Bài 3:
Cho đoạn thẳng có độ dài . Gọi là tâm đối xứng của đoạn thẳng . Tính độ dài đoạn thẳng
Bài 4:
Hình thoi có tâm đối xứng . Biết . Hãy tính diện tích hình thoi.
Lời giải chi tiết:
Bài 1:
Chữ cái nào trong mỗi từ sau có tính đối xứng? Với mỗi từ, hãy nêu tên tỉnh thành tương ứng:
a) H O A B I N H b) N G H E A N
c) B E N T R E d) B A C K A N
e) Q U A N G T R I g) D A N A N G
Phương pháp
Sử dụng lý thuyết tâm đối xứng, trục đối xứng của một hình.
Lời giải
Các chữ cái H, O, I vừa có trục đối xứng, vừa có tâm đối xứn.
Chữ cái A, C, E, T, M, U có trục đối xứng.
Chữ cái N có tâm đối xứng.
Tên các tỉnh tương ứng là:
a) Hòa Bình b) Nghệ An
c) Bến Tre d) Bắc Kạn
e) Quảng Trị g) Đà Nẵng
Bài 2:
Trong các hình dưới đây, hình nào có tâm đối xứng?
Phương pháp
Sử dụng định nghĩa tâm đối xứng
Lời giải

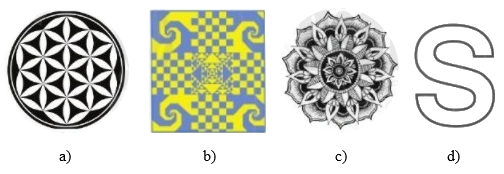
Hình a) có tâm đối xứng là điểm màu xanh có trong hình trên

Hình b) có tâm đối xứng là màu đỏ có trong hình trên
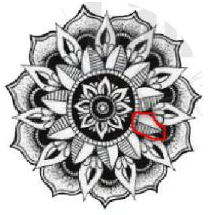
Hình c) không có tâm đối xứng vì số cánh hoa ở lớp thứ 2 (Loại cánh bị khoanh viền đỏ) là số lẻ. Nếu hình có tâm đối xứng thì đối diện của cánh hoa đó phải có 1 cánh hoa nữa nhưng điều này không xảy ra với hình trên.

Hình d) có tâm đối xứng là điểm màu đỏ.
Bài 3:
Cho đoạn thẳng có độ dài . Gọi là tâm đối xứng của đoạn thẳng . Tính độ dài đoạn thẳng
Phương pháp
Sử dụng lý thuyết tâm đối xứng.
Lời giải
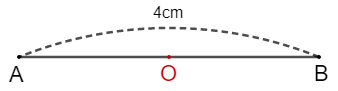
Vì là tâm đối xứng của đoạn thẳng nên .
Vậy .
Bài 4:
Hình thoi có tâm đối xứng . Biết . Hãy tính diện tích hình thoi.
Phương pháp
Sử dụng lý thuyết tâm đối xứng, công thức tính diện tích hình thoi.
Lời giải
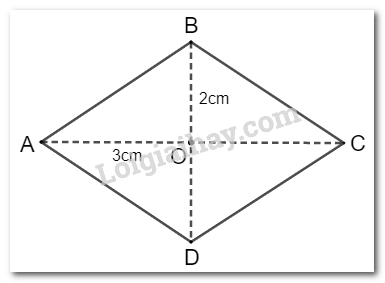
Vì là tâm đối xứng của hình thoi nên:
suy ra
suy ra
Độ dài hai đường chéo của hình thoi lần lượt là và .
Diện tích hình thoi là:



0 Comments:
Đăng nhận xét