Hợp số là gì? Hợp số là những số nào? Lấy ví dụ về hợp số?

 Hợp số là số nguyên dương chia hết cho các số nguyên dương nhỏ hơn 1 và chính nó. Các hợp số có thể được xác định bằng cách sử dụng phương pháp chia hết. Hãy tham khảo bài viết dưới đây để hiểu rõ hơn về hợp số.

Mục lục bài viết

Ẩn

• 1. Định Nghĩa Hợp Số:
• 2. Tìm Hợp Số:
• 3. Các loại hợp số:
  • 3.1. Hợp số lẻ:
  • 3.2. Hợp số chẵn:
  • 3.3. Tất cả các hợp số đến 100 là gì?
• 4. Phân biệt số nguyên tố và hợp số?
• 5. Các ví dụ có đáp án:

1. Định Nghĩa Hợp Số:

Trong toán học, hợp số có thể được định nghĩa là những số có nhiều hơn hai ước. Các số không phải là số nguyên tố là hợp số vì chúng chia hết cho nhiều hơn hai số.

Ví dụ:

Thừa số của 4 = 1, 2, 4. Vì 4 có nhiều hơn hai thừa số. Vậy 4 là hợp số.

Thừa số của 6 = 1, 2, 3, 6. Vì 6 cũng có nhiều hơn hai thừa số. Vậy 6 cũng là hợp số

Thừa số của 8 là 1, 2, 4 và 8. (1×8 = 8, 2×4 = 8). Vì 8 cũng có nhiều hơn hai thừa số. Vậy 8 cũng là hợp số

Thừa số của 9 là 1, 3 và 9. (1×9 = 9 và 3×3 = 9). Vì 9 cũng có nhiều hơn hai thừa số. Vậy 9 cũng là hợp số

Lưu ý:

– Các số 0 và 1 không phải là số nguyên tố cũng không phải là hợp số.

– Tất cả các số chẵn trừ 2 đều là hợp số.

– 4 là hợp số nhỏ nhất.

– Mỗi hợp số có thể viết được dưới dạng tích của hai hay nhiều số nguyên tố..

– Hợp số chia hết cho hợp số khác.

– Mọi hợp số luôn chia hết cho 1 và chính nó.

– Số nguyên tố nhỏ nhất = 2

– Hợp số lẻ nhỏ nhất = 9

– Hợp số nhỏ nhất có hai chữ số = 10

2. Tìm Hợp Số:

Cách tốt nhất để tìm ra một hợp số là thực hiện phép chia hết. Phép chia hết giúp ta nhận biết một số là số nguyên tố hay hợp số. Chia hết có nghĩa là một số được chia hoàn toàn (không có phần dư) cho một số khác, ngoài 1 và chính nó.

Ví dụ: 48 =2×2×2×2×3

Vì 48 chia hết cho 2 và 3 nên nó là hợp số.

299 là hợp số hay số nguyên tố?

Để bắt đầu, bạn phải xác định xem 299 có chia hết cho 2 hay không. Vì 299 là số lẻ nên chúng ta biết nó không chia hết cho 2. Bước tiếp theo là xác định xem 299 có chia hết cho 3 hay không… không phải vậy.

Sau đó, bạn phải xác định xem 299 có chia hết cho 5 hay không. Chúng ta biết 299 không chia hết cho 5 nếu không tính tổng vì nó không có tận cùng là 5 hoặc 0. Bây giờ chúng ta phải xác định xem 299 có chia hết cho 7 không .Tính nhanh ta thấy 299 không chia hết cho 7.

Đây là một ví dụ khó hơn vì 299 là một số lớn. Đây là một cơ hội tuyệt vời để kiểm tra khả năng phân chia của bạn. Nếu bạn tiếp tục chia 299 cho các số khác nhau, bạn sẽ phát hiện ra rằng nó có thể được chia thành 13 và 23. Điều này có nghĩa đó là một hợp số lẻ!

3. Các loại hợp số:

Có hai loại hợp số đó là

Thứ nhất là Hợp số lẻ

Thứ hai là Hợp số chẵn.

3.1. Hợp số lẻ:

Hợp số có chữ số lẻ ở hàng đơn vị là hợp số lẻ. Nói một cách đơn giản, tất cả các số lẻ không phải là số nguyên tố đều là hợp số lẻ. Ví dụ: 9, 15, 21, v.v.

3.2. Hợp số chẵn:

Hợp số có chữ số chẵn ở hàng đơn vị là hợp số chẵn. Nói một cách đơn giản, tất cả các số chẵn trừ 2 đều là hợp số chẵn. Điều này là do không có số chẵn nào (ngoại trừ 2) có thể là số nguyên tố.

Ví dụ: 8, 12, 14, v.v.

3.3. Tất cả các hợp số đến 100 là gì?

Đây là một lưới có các số từ 1-100. Được tô màu vàng nổi bật là tất cả các số ghép giúp bé dễ dàng ghi nhớ. Bạn có thể in nó ra và dán vào sách dành cho trẻ em hoặc đưa trang này cho con bạn xem như một công cụ hỗ trợ trực quan tuyệt vời:

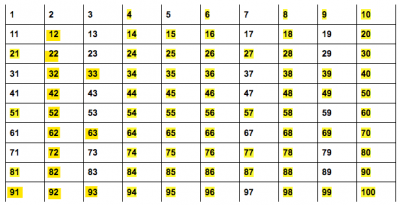
Học sinh sẽ không bắt buộc phải học thuộc lòng danh sách này. Sử dụng phép thử chia hết để tìm thừa số của một số rất hữu ích trong việc xác định một số là số nguyên tố hay hợp số.

Học sinh cần biết cách tìm các số nguyên tố đến 100 và biết các số nguyên tố đến 19. Các bài kiểm tra tính nguyên tố, chẳng hạn như phép chia thử nghiệm có thể là phương pháp mà học sinh sử dụng để tìm ra số nào là số nguyên tố cho đến số n, vì học sinh sẽ làm việc trong một phạm vi số lượng nhỏ.

Do đó, việc tìm các số nguyên tố dễ dàng hơn và biết rằng các số không phải là số nguyên tố được gọi là hợp số.

Làm thế nào để bạn giải thích các số tổng hợp cho trẻ em?

Bắt đầu bằng cách thực hiện từng bước một. Thông thường, trẻ em sẽ được làm quen với các số tổng hợp vào khoảng 7 hoặc 8 tuổi trong các bài học toán. Ở giai đoạn này, họ sẽ chỉ nắm bắt được một định nghĩa hợp số đơn giản.

Bạn có thể bắt đầu bằng cách sử dụng các phương tiện trực quan như bảng minh họa ở trên hoặc cung cấp cho trẻ bảng cửu chương cơ bản như ô vuông 100 trên và yêu cầu trẻ đánh dấu tất cả các số mà chúng nghĩ là hợp số.

Hãy thử và giải thích rằng mọi số lớn hơn một đều là hợp số hoặc số nguyên tố.

Ngoài ra còn có cách  để biết nếu một số là số nguyên tố

Để biết một số có phải là số nguyên tố hay không, bạn phải có khả năng biết nó có phải là số nguyên tố hay không. Dưới đây là một số cách dễ dàng mà bạn có thể biết nếu một số không phải là số nguyên tố:

– Theo quy tắc tiêu chuẩn, bất kỳ số nào lớn hơn 2, là bội số của 2 đều không phải là số nguyên tố. Điều này là do nó có ít nhất ba ước số: 1, 2 và chính nó. Do quy tắc này, chúng ta biết rằng 2 là số nguyên tố chẵn duy nhất.

– Nếu số đó lớn hơn 3 và là bội số của 3 thì đó không phải là số nguyên tố. Điều này là do nó có ít nhất ba ước số là 1, 3 và chính nó.

– Bất kỳ số nào là bội số của 4 cũng là bội số của 2, vì vậy nó có thể bị loại trừ là không phải là số nguyên tố.

– Bất kỳ số nào lớn hơn 5 và là bội số của 5 không phải là số nguyên tố. Điều này có nghĩa là số nguyên tố duy nhất kết thúc bằng 0 hoặc 5 chính là số 5

– Nếu một số là bội số của 6, thì nó cũng tự động là bội số của cả 2 và 3, vì vậy có thể loại trừ ngay lập tức nó không phải là số nguyên tố.

Về cơ bản, để biết một số có phải là số nguyên tố hay không, bạn phải xem tính chất chia hết của nó.

4. Phân biệt số nguyên tố và hợp số?

Số nguyên tố và hợp số là hai loại số khác nhau dựa trên số thừa số mà chúng có. Số nguyên tố là số chỉ có hai ước và hợp số có nhiều hơn hai ước. Thừa số là một giá trị, có thể chia đều một số hoặc một biểu thức.

Số nguyên tố là số có đúng hai ước là ‘1’ và chính số đó. Một hợp số có nhiều hơn hai thừa số, nghĩa là ngoài việc chia hết cho 1 và chính số đó, nó còn có thể chia hết cho ít nhất một số nguyên dương. 1 không phải là số nguyên tố hay hợp số. Ngoài hai số này, còn có một loại số tương tự là số nguyên tố cùng nhau.

Làm thế nào để biết một số là số nguyên tố hay hợp số?

Có một số thủ thuật và phương pháp để nhớ xem một số đã cho là số nguyên tố hay hợp số. Chúng ta có thể sử dụng phương pháp chia và Quy tắc chia hết để tìm xem một số có chia hết cho một hay nhiều số hay không. Ngoài ra, chúng ta có phương pháp phân tích thừa số nguyên tố để tìm các thừa số nguyên tố của các hợp số. Hãy xem cách hướng dẫn dưới đây:

– Nếu một số chia hết cho một số khác (khác 1) thì đó là hợp số

– Mọi số chẵn lớn hơn 2 đều là hợp số

– Số lớn hơn 2 và bội của 2 không phải là số nguyên tố mà là hợp số

– Tương tự, bội của bất kỳ số nào khác 1, không phải là số nguyên tố

– Nếu phép chia ra thừa số nguyên tố cho kết quả là tích của hai hay nhiều số nguyên tố thì đó là hợp số

– Ta có thể dùng quy tắc chia hết để kiểm tra xem một số có chia hết cho số khác hay không

5. Các ví dụ có đáp án:

Kiểm tra xem 104 có phải là hợp số hay không.

Số đã cho 104 chia hết cho 2 và do đó có nhiều hơn 2 ước.

Do đó, nó là một hợp số.

Kiểm tra xem 111 có phải là hợp số không.

Số đã cho chia hết cho 3 nên có nhiều hơn 2 ước.

Do đó, nó là một hợp số.

Kiểm tra xem 179 và 144 có phải là hợp số không.

Trong các số đã cho, 179 không chia hết cho số nào khác ngoài 1 và 179; do đó, nó không phải là một hợp số. 144 chia hết cho 2 nên nó là hợp số.

4. 0 có phải là hợp số không?

Số không (0) không được coi là số nguyên tố cũng không phải là hợp số vì nó không có bất kỳ ước nào.

Hợp số nhỏ nhất là?

4 là hợp số nhỏ nhất.

Tại sao?

1 không phải là hợp số vì ước duy nhất của 1 là 1. Các số nguyên dương 2 và 3 là số nguyên tố vì nó chỉ có thể chia hết cho hai thừa số là một và chính nó. Do đó 2 và 3 không phải là hợp số.

Nhưng trong trường hợp của số 4, chúng ta có nhiều hơn hai yếu tố. Các ước của 4 là 1,2,4. Vậy số này thỏa mãn điều kiện là hợp số như đã nêu ở trên. Sau 4, 6 là số nguyên dương tổng hợp tiếp theo có các thừa số là 1, 2, 3 và 6.

Vậy 4 là hợp số nhỏ nhất

Tìm tích của 5 hợp số đầu tiên.

5 hợp số đầu tiên là 4, 6, 8, 9, 10.

Do đó, tích của 5 số hỗn hợp đầu tiên = 4 × 6 × 8 × 9 × 10 = 17280

Vậy tích của 5 số tự nhiên đầu tiên là 17280.

Hệ số nguyên tố của 60 là gì?

Hệ số nguyên tố của 60 là: 60 = 2×2×3×5.

Liệt kê các hợp số trong tập hợp số đã cho.

2, 4, 9, 11, 21, 31, 44, 53, 67, 88, 101, 108.

Các hợp số là: 4, 9, 21, 44, 88, 108

Chen chọn một hợp số. Anh ta nhân nó với 10 và sau đó làm tròn nó đến hàng trăm gần nhất. Câu trả lời của anh ấy là 300. Viết tất cả các hợp số có thể mà Chen có thể đã chọn.

(Đáp án: 25, 26, 27, 28, 30, 32, 33, 34 )