Giải chuyên đề 5: Bài tập tự luyện: Phân số

Bài 22 : Hai chị em đi mua sách hết 112 000 đồng. Biết rằng

$\Large{\frac{3}{5}}$ số tiền sách của em bằng

$\Large{\frac{1}{3}}$ số tiền sách của anh. Hỏi mỗi người mua hết bao nhiêu tiền sách.

Phương pháp giải :
- Tìm số tiền sách của anh so với số tiền sách của em
- Tìm số tiền sách của mỗi người
Lời giải chi tiết : Số tiền sách của anh so với số tiền sách của em là

$\Large{\frac{3}{5}}$ x 3 =

$\Large{\frac{9}{5}}$ (số tiền sách của em)
Số tiền sách của anh là
112 000 : (9 + 5) x 9 = 72 000 (đồng)
Số tiền sách của em là
112 000 - 72 000 = 40 000 (đồng)
Đáp số: 40 000 đồng

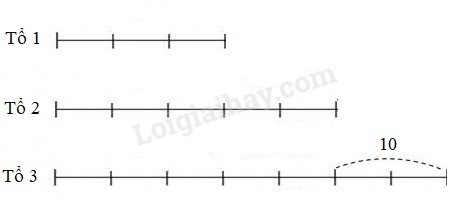
Bài 23 : Có 3 tổ công nhân sản xuất trong nhà máy. Biết rằng

$\Large{\frac{1}{3}}$ số người của tổ thứ nhất bằng

$\Large{\frac{1}{5}}$ số người của tổ thứ hai và bằng

$\Large{\frac{1}{7}}$ số người của tổ thứ ba. Tổ thứ ba nhiều hơn tổ thứ hai 10 người. Hỏi mỗi tổ có bao nhiêu người?

Bài 24 : Có hai thùng dầu chứa tổng cộng 54 lít. Người ta lấy ra ở thùng thứ nhất

$\Large{\frac{3}{7}}$ số dầu, lấy ở thùng thứ hai

$\Large{\frac{4}{5}}$ số dầu thì số dầu còn lại ở hai thùng bằng nhau. Hỏi mỗi thùng có bao nhiêu lít dầu?

Phương pháp giải :
- Tìm phân số chỉ số dầu còn lại ở mỗi thùng
- Tìm tỉ số số lít dầu ở thùng thứ hai so với thùng thứ nhất
- Giải bài toán tổng, tỉ để tìm số lít dầu ở mỗi thùng
Lời giải chi tiết :
Số dầu còn lại ở thùng thứ nhất là
1 -

$\Large{\frac{3}{7}}$ =

$\Large{\frac{4}{7}}$ (thùng thứ nhất)
Số dầu còn lại ở thùng thứ hai là
1 -

$\Large{\frac{4}{5}}$ =

$\Large{\frac{1}{5}}$ (thùng thứ hai)
Theo đề bài ta có:

$\Large{\frac{1}{5}}$ thùng thứ hai bằng

$\Large{\frac{4}{7}}$ thùng thứ nhất
Thùng dầu thứ hai so với thùng dầu thứ nhất thì bằng:

$\Large{\frac{4}{7}}$ x 5 =

$\Large{\frac{20}{7}}$ (thùng thứ nhất)
Coi số lít dầu ở thùng thứ nhất là 7 phần thì số lít dầu ở thùng thứ hai là 20 phần.
Tổng số phần bằng nhau là:
7 + 20 = 27 (phần)
Số lít dầu của thùng thứ nhất là
54 : 27 x 7 = 14 (lít)
Số lít dầu của thùng thứ hai là:
54 – 14 = 40 (lít)
Đáp số: Thùng thứ nhất: 14 lít
Thùng thứ hai: 40 lít

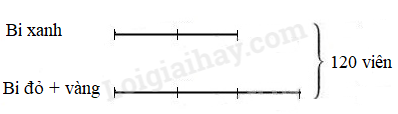
Bài 25 : Một hộp bi có ba màu: xanh, đỏ, vàng. Tổng cộng 120 viên bi. Biết rằng số bi xanh bằng

$\Large{\frac{2}{3}}$ tổng số bi đỏ và vàng, số bi vàng bằng

$\Large{\frac{4}{5}}$ số bi đỏ. Hỏi mỗi loại có bao nhiêu viên bi?

Bài 26 : Tỉ số học sinh nam so với nữ của trường Thắng Lợi đầu năm là

$\Large{\frac{3}{4}}$ . Nếu chuyển thêm 60 học sinh nam từ trường khác đến thì tỉ số giữa học sinh nam và nữ là

$\Large{\frac{9}{10}}$ .

Tìm số học sinh nữ của trường.

Phương pháp giải :
- Tìm 60 học sinh nam chuyển đến so với số học sinh nữ chiếm bao nhiêu phần
- Tìm số học nữ của trường đó
Lời giải chi tiết :
Lúc đầu số học sinh nam bằng

$\Large{\frac{3}{4}}$ số học sinh nữ. Lúc sau số học sinh nam bằng

$\Large{\frac{9}{10}}$ số học sinh nữ.
Vì số học sinh nữ không đổi, nên 60 học sinh nam chuyển đến so với số học sinh nữ chiếm số phần là:

$\Large{\frac{9}{10}}$ -

$\Large{\frac{3}{4}}$ =

$\Large{\frac{3}{20}}$ (số học sinh nữ)
Số học sinh nữ của trường đó là
60:

$\Large{\frac{3}{20}}$ = 400 (học sinh)
Đáp số: 400 học sinh nữ

Bài 27 : Khối 5 gồm 3 lớp có tất cả 102 học sinh. Biết tỉ số số học sinh 5B so với 5A là

$\Large{\frac{8}{9}}$ , tỉ số số học sinh 5C so với 5B là

$\Large{\frac{17}{6}}$ . Hãy tính số học sinh mỗi lớp.

Phương pháp giải :
Ta có

$\Large{\frac{8}{9}}$ =

$\Large{\frac{16}{18}}$
Theo đề bài tỉ số số học sinh 5B so với 5A là

$\Large{\frac{17}{6}}$
Nếu coi số học sinh lớp 5A là 18 phần thì số học sinh lớp 5B là 16 phần và số học sinh lớp 5C là 17 phần bằng nhau.
Tổng số phần bằng nhau là
18 + 16 + 17 = 51 (phần)
Số học sinh lớp 5A là
102 : 51 x 18 = 36 (học sinh)
Số học sinh lớp 5B là
102 : 51 x 16 = 32 (học sinh)
Số học sinh lớp 5C là
102 – (36 + 32) = 34 (học sinh)
Đáp số: 5A: 36 học sinh; 5B: 32 học sinh; 5C: 34 học sinh

Bài 28 : Một trang trại có 50 con gồm trâu và bỏ. Biết rằng nếu lấy

$\Large{\frac{2}{5}}$ số trâu cộng với

$\Large{\frac{3}{4}}$ số bò thì được 27 con. Hỏi trang trại có bao nhiêu con trâu, bao nhiêu con bò?

Phương pháp giải :
Theo đề bài ta có:
Số trâu + số bò = 50 con (1)

$\Large{\frac{2}{5}}$ số trâu +

$\Large{\frac{3}{4}}$ số bò = 27 con (2)
Nhân (1) với

$\Large{\frac{2}{5}}$ ta được:

$\Large{\frac{2}{5}}$ số trâu +

$\Large{\frac{2}{5}}$ số bò = 20 con (3)

$\Large{\frac{2}{5}}$ số trâu +

$\Large{\frac{3}{4}}$ số bò = 27 con (2)
Lấy (2) trừ đi (3) ta được:
(

$\Large{\frac{3}{4}}$ -

$\Large{\frac{2}{5}}$ )số bò = 7 con

$\Large{\frac{2}{20}}$

$\Large{\frac{2}{5}}$ = 7 con
Vậy số bò là 7 :

$\Large{\frac{7}{20}}$ = 20 (con)
Số trâu là 50 – 20 = 30 (con)
Đáp số: 20 con bò, 30 con trâu

Bài 29 : Hồng đi chợ đem theo 1 số tiền. Đầu tiên Hồng mua sách hết

$\Large{\frac{2}{3}}$ số tiền mang theo, sau đó mua vở hết

$\Large{\frac{3}{4}}$ số tiền còn lại, cuối cùng Hồng còn 6000 đồng. Hỏi Hồng đi chợ đem theo bao nhiêu tiền?

Phương pháp giải :
- Tìm phân số chỉ số tiền còn lại sau khi mua sách
- Tìm phân số chỉ số tiền mua vở
- Tìm phân số chỉ số tiền còn lại sau khi mua sách và vở
- Tìm số tiền Hồng mang theo
Lời giải chi tiết :
Số tiền còn lại sau khi mua sách là
1 -

$\Large{\frac{2}{3}}$ =

$\Large{\frac{1}{3}}$ (số tiền đem theo)
Số tiền mua vở bằng:

$\Large{\frac{3}{4}}$ x

$\Large{\frac{1}{3}}$ =

$\Large{\frac{1}{4}}$ (số tiền đem theo)
Số tiền còn lại sau khi mua sách và vở bằng:
1 - (

$\Large{\frac{2}{3}}$ +

$\Large{\frac{1}{4}}$ ) =

$\Large{\frac{1}{12}}$ (số tiền đem theo)
Số tiền Hồng đem theo là
6000:

$\Large{\frac{1}{12}}$ = 72 000 (đồng)
Đáp số: 72 000 đồng

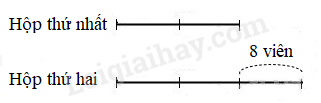
Bài 30: Có hai hộp phấn, hộp thứ nhất ít hơn hộp thứ hai 8 viên phấn, biết rằng

$\Large{\frac{3}{4}}$ số phấn trong hộp thứ nhất bằng

$\Large{\frac{1}{2}}$ số phấn của hộp thứ hai. Hỏi mỗi hộp có bao nhiêu viên phấn?

Phương pháp giải :
- Tìm tỉ số số viên phấn ở hộp thứ hai so với hộp thứ nhất =

$\Large{\frac{3}{4}}$ x 2 =

$\Large{\frac{3}{2}}$ (số phấn hộp thứ nhất)
Ta có sơ đồ:

Số viên phấn của hộp thứ nhất là 8 x 2 = 16 (viên)
Số viên phấn ở hộp thứ hai là
16 + 8 = 24 (viên phấn)
Đáp số: Hộp thứ nhất: 16 viên
Hộp thứ hai: 24 viên

Bài 31 : Một cửa hàng bán 1 bao đường làm ba lần. Lần thứ nhất cửa hàng bán

$\Large{\frac{1}{3}}$ bao đường và 5kg, lần thứ hai bán

$\Large{\frac{3}{7}}$ chỗ còn lại và 3kg, lần thứ ba bán 17 kg thì hết bao đường. Hỏi bao đường có bao nhiêu kilôgam?

Lời giải chi tiết :
Nếu lần thứ hai không bán thêm 3 kg đường thì số đường còn lại sau khi bán lần thứ hai là
17+ 3 = 20 (kg)
20 kg đường tương ứng với:
1 -

$\Large{\frac{3}{7}}$ =

$\Large{\frac{4}{7}}$ (số đường còn lại sau khi bán lần thứ nhất)
Số đường còn lại sau khi bán lần thứ nhất là
20 :

$\Large{\frac{4}{7}}$ = 35 (kg)
Nếu lần thứ nhất không bán thêm 5 kg thì số đường còn lại sau khi bán lần thứ nhất là
35 + 5 = 40 (kg)
40 kg đường bằng:
1 -

$\Large{\frac{1}{3}}$ =

$\Large{\frac{2}{3}}$ (bao đường)
Số đường có trong bao là:
40 :

$\Large{\frac{2}{3}}$ = 60 (kg)
Đáp số: 60 kg

Bài 32 : Hà đọc một quyển sách trong 3 ngày thì xong. Ngày thứ nhất Hà đọc được

$\Large{\frac{1}{3}}$ quyển. Ngày thứ hai Hà đọc

$\Large{\frac{4}{7}}$ số trang còn lại. Ngày thứ ba Hà đọc ít hơn ngày thứ hai là 40 trang. Tính số trang của quyển sách.

Phương pháp giải :
- Tìm phân số chỉ số trang sách Hà đọc trong ngày thứ hai và thứ ba
- Tìm 40 trang ứng với bao nhiêu phần cuốn sách
- Tìm số trang của cuốn sách
Lời giải chi tiết :
Số trang sách còn lại chưa đọc sau ngày thứ nhất là
1 -

$\Large{\frac{1}{3}}$ =

$\Large{\frac{2}{3}}$ (quyển sách)
Ngày thứ hai Hà đọc số trang sách bằng:

$\Large{\frac{4}{7}}$ x

$\Large{\frac{2}{3}}$ =

$\Large{\frac{8}{21}}$ (quyển sách)
Ngày thứ ba, Hà đọc số trang sách bằng:
1 - (

$\Large{\frac{1}{3}}$ +

$\Large{\frac{8}{21}}$ ) =

$\Large{\frac{2}{7}}$ (quyển sách)
40 trang sách bằng:

$\Large{\frac{8}{21}}$ -

$\Large{\frac{2}{7}}$ =

$\Large{\frac{2}{21}}$ (quyển sách)
Số trang của quyển sách là
40 :

$\Large{\frac{2}{21}}$ = 420 (trang)
Đáp số: 420 trang

Bài 33 : Một ô tô chạy quãng đường AB trong 3 giờ. Giờ đầu chạy được

$\Large{\frac{2}{5}}$ quãng đường AB. Giờ thứ hai chạy được

$\Large{\frac{2}{5}}$ quãng đường còn lại và thêm 4 km. Giờ thứ ba chạy nốt 50 km cuối. Tính quãng đường AB.

Lời giải chi tiết :
Nếu giờ thứ hai không chạy thêm 4 km thì quãng đường còn lại sau giờ thứ hai là:
50 + 4 = 54 (km)
Quãng đường xe chạy trong giờ thứ hai là
(1 -

$\Large{\frac{2}{5}}$ ) x

$\Large{\frac{2}{5}}$ =

$\Large{\frac{6}{25}}$ (quãng đường AB)
Quãng đường còn lại sau khi xe chạy 2 giờ là
1 - (

$\Large{\frac{2}{5}}$ +

$\Large{\frac{2}{25}}$ ) =

$\Large{\frac{9}{25}}$ (quãng đường AB)
Quãng đường AB dài là
50 :

$\Large{\frac{9}{25}}$ = 150(km)
Đáp số: 150 km

Bài 34 : Hai người làm chung một một công việc trong 12 giờ thì xong. Người thứ nhất làm một mình

$\Large{\frac{2}{3}}$ công việc thì mất 10 giờ. Hỏi người thứ hai làm

$\Large{\frac{1}{3}}$ công việc còn lại mất bao lâu?

Phương pháp giải :
- Tìm số phân công việc 2 người làm trong 1 giờ
- Tìm số phần công việc người thứ nhất làm trong 1 giờ
- Tìm số phần công việc người thứ hai làm trong 1 giờ
- Tìm số giờ để người thứ hai làm

$\Large{\frac{1}{3}}$ công việc còn lại
Lời giải chi tiết :
Trong 1 giờ hai người làm được số phần công việc là
1 : 12 =

$\Large{\frac{1}{12}}$ (công việc)
Trong 1 giờ người thứ nhất làm được số phần công việc là

$\Large{\frac{2}{3}}$ : 10 =

$\Large{\frac{1}{15}}$ (công việc)
Trong 1 giờ người thứ hai làm được số phần công việc là

$\Large{\frac{1}{12}}$ -

$\Large{\frac{1}{15}}$ =

$\Large{\frac{1}{60}}$ (công việc)
Người thứ hai làm

$\Large{\frac{1}{3}}$ công việc còn lại hết số giờ là:

$\Large{\frac{1}{3}}$ :

$\Large{\frac{1}{60}}$ = 20 (giờ)
Đáp số: 20 giờ

Bài 35 : Một người bán hết 63 kg gạo trong bốn lần. Lần đầu bán

$\Large{\frac{1}{2}}$ số gạo và

$\Large{\frac{1}{2}}$ kg gạo. Lần thứ hai bán

$\Large{\frac{1}{2}}$ số gạo còn lại và

$\Large{\frac{1}{2}}$ kg gạo. Lần thứ ba bán

$\Large{\frac{1}{2}}$ số gạo còn lại sau hai lần bán và

$\Large{\frac{1}{2}}$ kg gạo. Hỏi lần thứ tư người đó bán được bao nhiêu ki-lô-gam gạo?

Lời giải chi tiết :
Ngày đầu bán số kg gạo là
63 x

$\Large{\frac{1}{2}}$ +

$\Large{\frac{1}{2}}$ = 32 (kg)
Ngày thứ hai bán số kg gạo là
(63 - 32) x

$\Large{\frac{1}{2}}$ +

$\Large{\frac{1}{2}}$ = 16(kg)
Ngày thứ ba bán được số kg là
(63 - 32 - 16) x

$\Large{\frac{1}{2}}$ +

$\Large{\frac{1}{2}}$ = 8(kg)
Ngày thứ tư bán được số kg là
63 – (32 + 16 + 8) = 7 (kg)
Đáp số: 7 kg

Bài 36 : Lớp 5A có số học sinh nữ bằng

$\Large{\frac{1}{3}}$ số học sinh nam. Sau bài thi chuyên đề, có 3 học sinh nữ chuyển lớp và thay vào đó là 3 học sinh nam lớp khác do đó số học sinh nữ bằng

$\Large{\frac{1}{6}}$ số học sinh nam. Tính số học sinh lớp 5A.

Lời giải chi tiết :
Lúc đầu số học sinh nữ bằng

$\Large{\frac{1}{3}}$ số học sinh nam hay số học sinh nữ bằng

$\Large{\frac{1}{4}}$ số học sinh cả lớp.
Sau khi chuyển lớp, số học sinh nữ bằng

$\Large{\frac{1}{6}}$ số học sinh nam hay số học sinh nữ bằng

$\Large{\frac{1}{7}}$ số học sinh cả lớp.
Vì số học sinh cả lớp không đổi nên 3 học sinh nữ chuyển đi so với số học sinh cả lớp bằng:

$\Large{\frac{1}{4}}$ -

$\Large{\frac{1}{7}}$ =

$\Large{\frac{3}{28}}$ (số học sinh cả lớp)
Số học sinh lớp 5A là
3 :

$\Large{\frac{3}{28}}$ = 28 (học sinh)
Đáp số: 28 học sinh

Bài 37: Cả ba tấm vải dài tổng cộng 117m. Nếu cắt bớt

$\Large{\frac{3}{7}}$ tấm vải xanh,

$\Large{\frac{1}{5}}$ tấm vải đỏ và

$\Large{\frac{1}{3}}$ tấm vải trắng thì phần còn lại của 3 tấm vải dài bằng nhau. Tính chiều dài mỗi tấm vải?

Phương pháp giải :
- Tìm phân số chỉ số phần tấm vải sau khi cắt bớt
- Coi tấm vải xanh là 7 phần bằng nhau, tấm vải đỏ là 5 phần bằng nhau, tấm vải trắng là 6 phần bằng nhau.
- Giải bài toán tổng - tỉ để tìm chiều dài mỗi tấm vải.
Lời giải chi tiết :
Sau khi cắt ba tấm vải ta có:
Tấm vải xanh còn lại là
1 -

$\Large{\frac{3}{7}}$ =

$\Large{\frac{4}{7}}$ (tấm vải xanh)
Tấm vải đỏ còn lại là 1 -

$\Large{\frac{1}{5}}$ =

$\Large{\frac{4}{5}}$ (tấm vải đỏ)
Tấm vải trắng còn lại là
1 -

$\Large{\frac{1}{3}}$ =

$\Large{\frac{2}{3}}$ =

$\Large{\frac{4}{6}}$ (tấm vải trắng)
Ta có

$\Large{\frac{4}{7}}$ tấm vải xanh =

$\Large{\frac{4}{5}}$ tấm vải đỏ =

$\Large{\frac{4}{6}}$ tấm vải trắng
Coi tấm vải xanh là 7 phần bằng nhau, tấm vải đỏ là 5 phần bằng nhau, tấm vải trắng là 6 phần bằng nhau.
Tổng số phần bằng nhau là
7 + 5 + 6 = 18 (phần)
Vậy tấm vải xanh dài là
117 : 18 x 7 = 45,5 (m)
Tấm vải đỏ dài là
117 : 18 x 5 = 32,5 (m)
Tấm vải trắng dài là
117 – (45,5 + 32,5) = 39 (m)
Đáp số: Vải xanh 45,5m; Vải đỏ 32,5 m; Vải trắng 39m

Bài 38 : Bốn người góp vốn thành lập một công ty. Người thứ nhất góp 64 triệu đồng; người thứ hai góp bằng

$\Large{\frac{2}{3}}$ số tiền của ba người còn lại; người thứ ba góp

$\Large{\frac{1}{4}}$ bằng số tiền của ba người còn lại và người thứ tư góp bằng

$\Large{\frac{2}{5}}$ số tiền của ba người còn lại. Hỏi mỗi người đã góp bao nhiêu tiền?

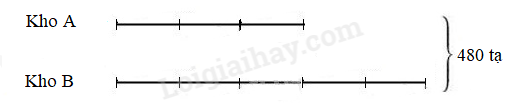
Bài 39 : Hai kho có tất cả 450 tạ thóc. Sau khi kho A nhập thêm 55 tạ thóc và kho B xuất đi 25 tạ thóc thì số thóc của kho A bằng

$\Large{\frac{3}{5}}$ số thóc kho B. Hỏi lúc đầu mỗi kho có bao nhiêu tạ thóc?

Bài 40 : Ba lớp 5 có tất cả 63 học sinh đạt học sinh giỏi. Số học sinh giỏi của lớp 5A bằng

$\Large{\frac{3}{4}}$ số học sinh giỏi của lớp 5B. Số học sinh giỏi của lớp 5C bằng

$\Large{\frac{4}{5}}$ số học sinh giỏi của lớp 5A. Hỏi mỗi lớp có bao nhiêu học sinh giỏi?

Phương pháp giải :
- Số học sinh giỏi của lớp 5A bằng

$\Large{\frac{3}{4}}$ =

$\Large{\frac{6}{8}}$ số học sinh giỏi của lớp 5B
- Tìm tỉ số số học sinh giỏi của lớp 5C so với lớp 5B
- Giải bài toán tổng tỉ để tìm số học sinh của mỗi lớp
Lời giải chi tiết :
Ta có: số học sinh giỏi của lớp 5A bằng

$\Large{\frac{3}{4}}$ =

$\Large{\frac{6}{8}}$ số học sinh giỏi của lớp 5B, số học sinh giỏi của lớp 5C bằng

$\Large{\frac{7}{6}}$ số học sinh giỏi của lớp 5A.
Vậy số học sinh giỏi của lớp 5C so với lớp 5B là

$\Large{\frac{7}{6}}$ x

$\Large{\frac{6}{8}}$ =

$\Large{\frac{7}{8}}$ (số học sinh giỏi lớp 5B)
Coi số học sinh giỏi của lớp 5B là 8 phần thì số học sinh giỏi của lớp 5A là 6 phần, số học sinh giỏi của lớp 5C là 7 phần.
Tổng số phần bằng nhau là
        8 + 6 + 7 = 21 (phần)
Số học sinh giỏi lớp 5A là
  63 : 21 x 6 = 18 (học sinh)
Số học sinh giỏi của lớp 5B là
  63 : 21 x 8 = 24 (học sinh)
Số học sinh giỏi của lớp 5C là
  63 – (18 + 24) = 21 (học sinh)
Đáp số: Lớp 5A: 18 học sinh
               Lớp 5B: 24 học sinh
               Lớp 5C: 21 học sinh

Bài 41 : Ba xe ô tô chở 98 học sinh đi tham quan, biết

$\Large{\frac{2}{3}}$ số học sinh ở xe thứ nhất bằng

$\Large{\frac{3}{4}}$ số học sinh ở xe thứ hai và bằng

$\Large{\frac{4}{5}}$ số học sinh ở xe thứ ba. Hỏi mỗi xe chở bao nhiêu học sinh?

Phương pháp giải :
- Quy đồng tử số các phân số với tử số chung là 12
- Giải bài toán tổng - tỉ để tìm số học sinh ở mỗi xe
Lời giải chi tiết :
Có

$\Large{\frac{2}{3}}$ số học sinh ở xe thứ nhất bằng

$\Large{\frac{3}{4}}$ số học sinh ở xe thứ hai và bằng

$\Large{\frac{4}{5}}$ số học sinh ở xe thứ ba.
Quy đồng tử số các phân số ta được:

$\Large{\frac{12}{18}}$ số học sinh ở xe thứ nhất =

$\Large{\frac{12}{16}}$ số học sinh ở xe thứ hai =

$\Large{\frac{12}{15}}$ số học sinh ở xe thứ ba

Gọi số học sinh ở xe thứ nhất là 18 phần bằng nhau thì số học sinh ở xe thứ hai là 16 phần và số học sinh ở xe thứ ba là 15 phần.

Tổng số phần bằng nhau là
  18+ 16 + 15 = 49 (phần)
Xe thứ nhất chở số học sinh là
  98 : 49 x 18 = 36 (học sinh)
Xe thứ hai chở số học sinh là
  98 : 49 x 16 = 32 (học sinh)
Xe thứ ba chở số học sinh là
  98 – (36 + 32) = 30 (học sinh)
Đáp số:   Xe thứ nhất: 32 học sinh     Xe thứ hai: 32 học sinh     Xe thứ ba: 30 học sinh

Giải chuyên đề 5: Bài tập tự luyện: Phân số

0 Comments:

Đăng nhận xét

Giải chuyên đề 5: Bài tập tự luyện: Phân số

Next

Giải chuyên đề 5: Dạng 2: Các bài toán về thêm, bớt ở tử số và mẫu số

Previous

Giải chuyên đề 6: Dạng 1: Các bài toán về đại lượng tỉ lệ thuận

0 Comments:

Đăng nhận xét