Cho phân số $\Large{\frac{56}{81}}$=. Hỏi cùng thêm vào tử số và mẫu số bao nhiêu đơn vị để được phân số bằng $\Large{\frac{3}{4}}$.
Cho phân số $\Large{\frac{23}{45}}$. Hỏi phải cộng thêm vào tử số và bớt đi ở mẫu số cùng một số tự nhiên nào để được phân số mới có giá trị bằng $\Large{\frac{19}{15}}$
Phương pháp giải
- Nếu ta cộng thêm (hoặc trừ đi) cả tử số và mẫu số của một phân số với cùng một số tự nhiên thì hiệu của tử số và mẫu số của phân số đó không thay đổi.
- Nếu cộng thêm vào tử số đồng thời bớt đi ở mẫu số của một phân số với cùng một số tự nhiên thì tổng của tử số và mẫu số không thay đổi.
- Nếu ta bớt đi ở tử số đồng thời thêm vào mẫu số của một phân số với cùng một số tự nhiên thì tổng của tử số và mẫu số không thay đổi.
Ví dụ 1: Cho phân số . Hỏi cùng thêm vào tử số và mẫu số bao nhiêu đơn vị để được phân số bằng $\Large{\frac{3}{4}}$
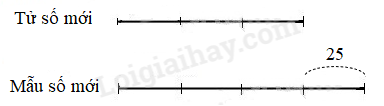
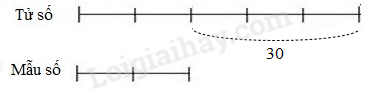
Ví dụ 2: Cho phân số $\Large{\frac{23}{45}}$. Hỏi phải cộng thêm vào tử số và bớt đi ở mẫu số cùng một số tự nhiên nào để được phân số mới có giá trị bằng $\Large{\frac{19}{15}}$
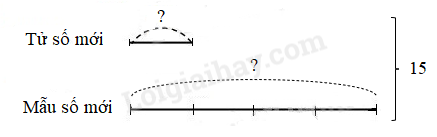
Ví dụ 3: Cho phân số $\Large{\frac{26}{45}}$ . Hãy tìm số tự nhiên c sao cho đem mẫu số của phân số đã cho trừ đi c và giữ nguyên tử số ta được phân số mới có giá trị bằng $\Large{\frac{5}{6}}$
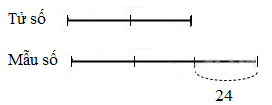
Ví dụ 4: Cho phân số $\Large{\frac{26}{45}}$. Hãy tìm số tự nhiên c sao cho thêm c vào tử số và giữ nguyên mẫu số, ta được phân số mới có giá trị bằng $\Large{\frac{2}{3}}$
Bài tập áp dụng
Bài 1 : Cho phân số $\Large{\frac{3}{7}}$. Cộng thêm vào cả tử số và mẫu số cùa phân số đó với cùng một số tự nhiên ta được một phân số bằng $\Large{\frac{7}{9}}$.
. Tìm số tự nhiên đó.
Bài 2 : Khi bớt cả tử số và mẫu số của phân số $\Large{\frac{71}{41}}$ đi cùng một số tự nhiên ta nhận được một phân số bằng $\Large{\frac{5}{2}}$. Tìm số tự nhiên đó.
Bài 3 : Cho phân số $\Large{\frac{7}{8}}$. Hãy tìm số a sao cho đem tử số của phân số đã cho trừ đi a và thêm a vào mẫu số ta được một phân số mới bằng $\Large{\frac{1}{4}}$.
Bài 4 : Cho phân số $\Large{\frac{a}{b}}$. Rút gọn phân số $\Large{\frac{a}{b}}$ ta được phân số $\Large{\frac{2}{5}}$. Nếu thêm vào tử số 45 đơn vị thì ta được phân số mới có giá trị bằng $\Large{\frac{13}{20}}$. Tìm phân số $\Large{\frac{a}{b}}$
Bài 5 : Cho phân số $\Large{\frac{73}{97}}$. Hỏi cùng phải bớt ở tử số và mẫu số bao nhiêu đơn vị để được phân số mới có giá trị bằng $\Large{\frac{2}{3}}$
BÀI TẬP TỰ LUYỆN
Bài 1 : Hãy chứng tỏ rằng các phân số sau bằng nhau:
a) $\Large{\frac{123}{127}}$ = $\Large{\frac{123123}{127127}}$
b) $\Large{\frac{13}{15}}$ = $\Large{\frac{1313}{1515}}$ = $\Large{\frac{131313}{151515}}$
Bài 2 : Tính nhanh:
a) $\Large{\frac{2006 \times 2005 -1}{2004 \times 2006 + 2005}}$
b) $\Large{\frac{1999 \times 2001-1}{1998 + 1999 \times 2000}}$ \times $\Large{\frac{7}{5}}$
c) $\Large{\frac{1313}{2121}}$ \times $\Large{\frac{165165}{143143}}$ \times $\Large{\frac{424242}{151515}}$
d) $\Large{\frac{1995 \times 1993 - 18}{1975 + 1993 \times 1994}}$
Bài 4 : Tính nhanh:
a) A = $\Large{\frac{6 \times 7 \times 8 \times 9 \times 10 \times 11}{22 \times 20 \times 18 \times 16 \times 14 \times 12}}$
b) (1 - $\Large{\frac{1}{2}}$) x (1 - $\Large{\frac{1}{3}}$) x (1 - $\Large{\frac{1}{4}}$) x (1 - $\Large{\frac{1}{5}}$) x(1 - $\Large{\frac{1}{5}}$)
Bài 4 : Tính:
a) A = $\Large{\frac{1}{20}}$ + $\Large{\frac{1}{30}}$ + $\Large{\frac{1}{42}}$ + $\Large{\frac{1}{56}}$ + $\Large{\frac{1}{72}}$+ $\Large{\frac{1}{90}}$
b) B = $\Large{\frac{3}{1 \times 3}}$ + $\Large{\frac{3}{1 \times 3}}$ + $\Large{\frac{3}{1 \times 3}}$ + $\Large{\frac{3}{3 \times 5}}$ + $\Large{\frac{3}{5 \times 7}}$ + ......+ $\Large{\frac{3}{99 \times 101}}$
Bài 5 : Tính M = 1$\Large{\frac{3}{34}}$ x 10$\Large{\frac{1}{12}}$ x $\Large{\frac{8}{9}}$ x 2$\Large{\frac{1}{8}}$ x $\Large{\frac{3}{13}}$ x $\Large{\frac{26}{37}}$ x 1$\Large{\frac{1}{19}}$ x $\Large{\frac{3}{4}}$
Bài 6 : (Cầu Giấy 2013 – 2014)
Tính A = ($\Large{\frac{3}{10}+ \frac{4}{5} \times \frac{1}{2}}$) : (2$\Large{\frac{8}{9}}$ - 1$\Large{\frac{1}{3}}$) + 2013
Bài 7 : (LTV 2014 – 2015)
Tính giá trị của biểu thức A = 17 ×($\Large{\frac{1313}{5151}+ \frac{111}{3434} }$): $\Large{\frac{177}{12}}$
Bài 8 : (ASM 2011 – 2012)
Tìm x sao cho: (x + $\Large{\frac{1}{1 \times 3}}$) + (x + $\Large{\frac{1}{3 \times 5}}$) + (x + $\Large{\frac{1}{5 \times 7}}$) ....+ (x + $\Large{\frac{1}{1 \times 3}}$)
= 11 $\times$ x + ($\Large{\frac{1}{3}}$ + $\Large{\frac{1}{9}}$ + $\Large{\frac{1}{27}}$+ $\Large{\frac{1}{81}}$ + $\Large{\frac{1}{243}}$)
Bài 9 : (NTT 2019 – 2020)
Một đội tự nguyện trường Nguyễn Tất thành đi trồng cây ở tỉnh Hà Giang trong 3 ngày. Ngày 1, đội trồng $\Large{\frac{1}{3}}$ số cây. Ngày 2, đội trồng $\Large{\frac{6}{11}}$ số cây còn lại. Ngày 3, trồng ít hơn ngày 2 là 30 cây. Tính số cây mà mỗi đội đã trồng được.
Bài 10 : (Cầu Giấy 2019 – 2020)
Cho một số bóng xanh và vàng. Số bóng vàng bằng $\Large{\frac{1}{3}}$ bóng xanh. Nếu thêm 6 bóng vàng thì bóng vàng bằng $\Large{\frac{5}{9}}$ bóng xanh. Tính số bóng xanh.
Bài 11 : (ASM 2019 – 2020)
Cho phân số $\Large{\frac{14}{17}}$. Hỏi cùng thêm vào cả tử số và mẫu số bao nhiêu đơn vị để được phân số mới có giá trị bằng $\Large{\frac{6}{7}}$
Bài 12 : Cửa hàng có một số hộp sữa đã bán hết trong 4 ngày. Ngày đầu bán $\Large{\frac{1}{3}}$ số hộp sữa. Ngày thứ hai bán $\Large{\frac{1}{3}}$ số hộp sữa còn lại. Ngày thứ ba bán $\Large{\frac{1}{3}}$ số hộp sữa còn lại sau 2 ngày. Ngày thứ tư bán 16 hộp thì hết. Hỏi cả 4 ngày cửa hàng bán hết bao nhiêu hộp sữa?
Bài 13 : Cho phân số $\Large{\frac{65}{34}}$. Hãy tìm số tự nhiên a sao cho khi bớt a ở tử số và thêm a vào mẫu số ta được phân số mới, rút gọn phân số mới ta được phân số $\Large{\frac{4}{5}}$.
Bài 14 : Cho phân số $\Large{\frac{234}{369}}$. Hỏi cùng phải bớt ở tử số và mẫu số bao nhiêu đơn vị để được phân số mới và rút gọn phân số mới đó ta được phân số $\Large{\frac{5}{8}}$
Bài 15 : Cho phân số $\Large{\frac{a}{b}}$. Rút gọn phân số $\Large{\frac{a}{b}}$ ta được phân số $\Large{\frac{5}{7}}$ . Nếu thêm 71 vào tử số và giữ nguyên mẫu số, ta được phân số $\Large{\frac{18}{11}}$. . Tìm phân số $\Large{\frac{a}{b}}$
Bài 16 : Cho phân số $\Large{\frac{12}{21}}$. Hỏi phải cùng thêm vào tử số và mẫu số của phân số này bao nhiêu đơn vị để được phân số bằng $\Large{\frac{8}{11}}$
Bài 17 : Một người bán hàng vải, lần thứ nhất bán $\Large{\frac{1}{2}}$ tấm vải, lần thứ hai bán $\Large{\frac{1}{3}}$ tấm vải đó thì tấm vải chỉ còn lại 7 m. Hỏi tấm vải đó dài bao nhiêu mét?
Bài 18 : Một thửa ruộng năm nay thu hoạch nhiều hơn năm ngoái 30 tạ. Biết $\Large{\frac{1}{7}}$ số thu hoạch năm ngoái thì bằng $\Large{\frac{1}{12}}$ số thu hoạch năm nay. Hỏi năm nay thu hoạch ở thửa ruộng đó được bao nhiêu tạ?
Bài 19 : Một người bán trứng bán lần thứ nhất $\Large{\frac{1}{5}}$ số trứng, lần thứ hai bán $\Large{\frac{3}{8}}$ số trứng thì còn lại 17 quả. Hỏi người đó đem bán bao nhiêu quả trứng và mỗi lần bán bao nhiêu quả?
Bài 20 : Hai chị em được 110 000 đồng tiền mừng tuổi. Nếu chị cho em 2000 đồng thì số tiền của chị bằng $\Large{\frac{5}{6}}$ số tiền của em. Hỏi mỗi người được bao nhiêu tiền mừng tuổi.



0 Comments:
Đăng nhận xét