12a

Bài 12 trang 89 Toán 8 Tập 1:
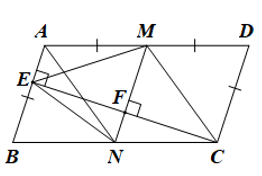
Cho hình bình hành ABCD có AD = 2AB. Từ C vẽ CE vuông góc với AB tại E. Nối E với trung điểm M của AD. Từ M vẽ MF vuông góc với CE tại F, MF cắt BC tại N.
    a) Tứ giác MNCD là hình gì?
    b) Chứng minh tam giác EMC cân tại M.
    c) Chứng minh rằng $\widehat{BAD}$ = 2 $\widehat{AEM}$ .

Hướng dẫn:
    b) Chứng minh EN = NC = NB = $\frac{1}{2}$ BC .
    c) Chứng minh $\widehat{AEM}$ = $\widehat{EMN}$ = $\widehat{NMC}$ = $\widehat{MCD}$ = 1 2 $\widehat{NCD}$ .

 Lời giải:

a) Tứ giác MNCD là hình gì?

• Do ABCD là hình bình hành nên AB // CD và AD // BC.
    Ta có AB ⊥ CE và MN ⊥ CE nên AB // MN
    Mà AB // CD nên MN // CD.
    Xét tứ giác MNCD có MN // CD và MD // CN (do AD // BC)
    Suy ra MNCD là hình bình hành.

• Ta có M là trung điểm của AD nên MA=MD=$\frac{1}{2}$AD hay AD = 2MD
    Mà AD = 2AB nên AB = MD
    Lại có AB = CD (do ABCD là hình bình hành)
    Do đó MD = CD.

• Hình bình hành MNCD có MD = CD nên MNCD là hình thoi.

b) Chứng minh tam giác EMC cân tại M.
• Do MNCD là hình thoi nên MD=CD=NC=MN=$\frac{1}{2}$AD=$\frac{1}{2}$BC (do AD = BD).
    Do NC=$\frac{1}{2}$BC nên N là trung điểm của BC.

• Xét DEBC vuông tại E có EN là đường trung tuyến ứng với cạnh huyền BC nên bằng nửa cạnh huyền BC
    Suy ra EN=NB=NC=$\frac{1}{2}$BC

• Do NE = NC nên N nằm trên đường trung trực của đoạn thẳng EC
    Hay đường trung trực của EC đi qua N và vuông góc với EC.
    Lai có NF ⊥ EC nên NF là đường trung trực của đoạn thẳng BC.
    Suy ra F là trung điểm của EC hay FE = FC.

• Xét DEMF và DCMF có:
$\widehat{MFE}$=$\widehat{MFC}$=90°
    MF là cạnh chung;
    FE = FC (chứng minh trên).
    Do đó DEMF = DCMF (hai cạnh góc vuông).
    Suy ra ME = MC (hai cạnh tương ứng)

    Tam giác EMC có ME = MC nên là tam giác cân tại M.

c) Chứng minh rằng $\widehat{BAD}$ = 2 $\widehat{AEM}$ .
• Vì AB // MN (chứng minh ở câu a) nên $\widehat{AEM}$=$\widehat{EMF}$ (so le trong)
    Ta có DEMF = DCMF (chứng minh ở câu b) nên $\widehat{EMF}$=$\widehat{CMF}$
    Do đó $\widehat{AEM}$=$\widehat{CMF}$(=$\widehat{EMF}$) .

• Do MNCD là hình thoi nên MC là đường phân giác của góc DMN
    Suy ra $\widehat{CMF}$=$\frac{1}{2}$$\widehat{DMN}$ , nên $\widehat{AEM}$=$\widehat{CMF}$=$\frac{1}{2}$$\widehat{DMN}$ (1)

• Do DMNC là hình thoi nên $\widehat{DMN}$=$\widehat{DCN}$ (hai góc đối bằng nhau)
    Do ABCD là hình bình hành nên $\widehat{BAD}$=$\widehat{DCB}$ (hai góc đối bằng nhau)
    Do đó $\widehat{DMN}$=$\widehat{BAD}$(=$\widehat{DCN}$) (2)
    Từ (1) và (2) ta có $\widehat{AEM}$=$\frac{1}{2}$$\widehat{BAD}$ hay $\widehat{BAD}$=2$\widehat{AEM}$ .