12b

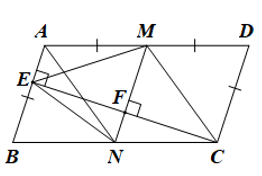
a) Tứ giác MNCD là hình gì?

• Do ABCD là hình bình hành nên AB // CD và AD // BC.
    Ta có AB ⊥ CE và MN ⊥ CE nên AB // MN
    Mà AB // CD nên MN // CD.
    Xét tứ giác MNCD có MN // CD và MD // CN (do AD // BC)
    Suy ra MNCD là hình bình hành.

• Ta có M là trung điểm của AD nên MA=MD=$\frac{1}{2}$AD hay AD = 2MD
    Mà AD = 2AB nên AB = MD
    Lại có AB = CD (do ABCD là hình bình hành)
    Do đó MD = CD.

• Hình bình hành MNCD có MD = CD nên MNCD là hình thoi.

b) Chứng minh tam giác EMC cân tại M.
• Do MNCD là hình thoi nên MD=CD=NC=MN=$\frac{1}{2}$AD=$\frac{1}{2}$BC (do AD = BD).
    Do NC=$\frac{1}{2}$BC nên N là trung điểm của BC.

• Xét DEBC vuông tại E có EN là đường trung tuyến ứng với cạnh huyền BC nên bằng nửa cạnh huyền BC
    Suy ra EN=NB=NC=$\frac{1}{2}$BC

• Do NE = NC nên N nằm trên đường trung trực của đoạn thẳng EC
    Hay đường trung trực của EC đi qua N và vuông góc với EC.
    Lai có NF ⊥ EC nên NF là đường trung trực của đoạn thẳng BC.
    Suy ra F là trung điểm của EC hay FE = FC.

• Xét DEMF và DCMF có:
$\widehat{MFE}$=$\widehat{MFC}$=90°
    MF là cạnh chung;
    FE = FC (chứng minh trên).
    Do đó DEMF = DCMF (hai cạnh góc vuông).
    Suy ra ME = MC (hai cạnh tương ứng)

    Tam giác EMC có ME = MC nên là tam giác cân tại M.

c) Chứng minh rằng $\widehat{BAD}$ = 2 $\widehat{AEM}$ .
• Vì AB // MN (chứng minh ở câu a) nên $\widehat{AEM}$=$\widehat{EMF}$ (so le trong)
    Ta có DEMF = DCMF (chứng minh ở câu b) nên $\widehat{EMF}$=$\widehat{CMF}$
    Do đó $\widehat{AEM}$=$\widehat{CMF}$(=$\widehat{EMF}$) .

• Do MNCD là hình thoi nên MC là đường phân giác của góc DMN
    Suy ra $\widehat{CMF}$=$\frac{1}{2}$$\widehat{DMN}$ , nên $\widehat{AEM}$=$\widehat{CMF}$=$\frac{1}{2}$$\widehat{DMN}$ (1)

• Do DMNC là hình thoi nên $\widehat{DMN}$=$\widehat{DCN}$ (hai góc đối bằng nhau)
    Do ABCD là hình bình hành nên $\widehat{BAD}$=$\widehat{DCB}$ (hai góc đối bằng nhau)
    Do đó $\widehat{DMN}$=$\widehat{BAD}$(=$\widehat{DCN}$) (2)
    Từ (1) và (2) ta có $\widehat{AEM}$=$\frac{1}{2}$$\widehat{BAD}$ hay $\widehat{BAD}$=2$\widehat{AEM}$ .